Hello Years 7 – 13,
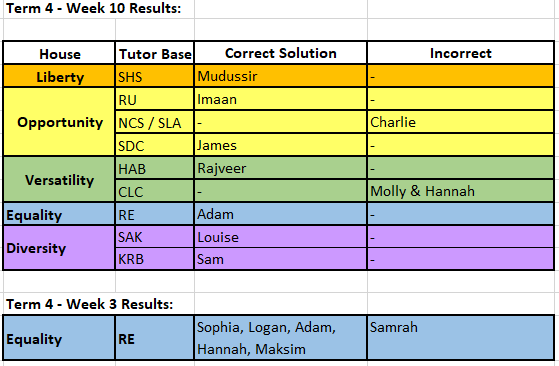
Well done to all those in the table below who entered last week’s Maths Challenge and earned those all-important house points. There were lots of correct entries to last week’s problem but pleased don’t be disheartened if yours was incorrect as there were some staggeringly large numbers, which can be difficult to interpret. So here’s the answer:
The number of pennies on the 64th square of a chess board would be sixty-three 2s multiplied together. It’s called 2 to the power of 63 and it is equal to 9,223,372,036,854,775,808 – that’s about 92 million billion pounds. It’s hard to believe that this can happen if we start off with just 1p on the first square and double each time!!
Supposing we put all the pennies in one tall thin pile, the 21st square would have over a million pennies on it and be about a mile (1.6 km) high. The pennies on the 39th square would reach the moon. The pennies on the 48th square would go beyond the sun and the pile of pennies on the 64th square would be about 1.5 light years high (much further than Pluto and about a third of the distance to our nearest star, Alpha Centauri).
There is no Maths challenge this week as it is the last week of term. Look out for the new challenges next term!
Mrs Uff 😊
P.S. RE’s Tutor Base: I have now received your entries from Week 3 (just before lockdown), which are shown underneath the table. Your house points will be added to the total.